Using PocketLab to Teach MS-PS2-1: Engineering Design and Newton's Third Law
NGSS Standard MS-PS2-1: What's in the standard?
Teaching NGSS Standard MS-PS2-1 can have challenges. Students need to apply principles in forces and motion to engineer a design that will solve a problem. The performance expectation for the standard states: Apply Newton’s Third Law to design a solution to a problem involving the motion of two colliding objects. Like all NGSS standards, the performance expectation is derived from three pillars, Science and Engineering Practices, Disciplinary Core Ideas, and Crosscutting Concepts.
For MS-PS2-1 the three NGSS pillars are broken down below:
Science and Engineering Practices: Constructing explanations and designing solutions.
The Disciplinary Core Ideas: PS2.A: Forces and Motion (Newton's Third Law)
Crosscutting Concepts: Systems and System Models
For a more detailed look at the standard, click here.
Teaching MS-PS2-1 with PocketLab: Crash Cushions and Bumper Design
In the lessons linked below, students design and build crash cushion models to reduce the impact force of a cart in a collision. This activity helps students meet the NGSS MS-PS2-1 performance expectation.
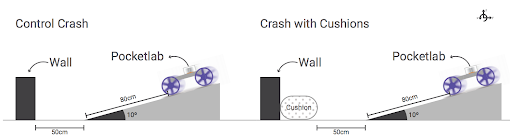
The design challenge models real-world problems that engineers face when designing crash cushions along highways. Students crash a cart into a wall. A PocketLab is attached to the cart. The PocketLab measures the acceleration of the cart at impact. They then design crash cushions to reduce the impact force felt by the cart during the collision.
Students can do a similar version of this experiment where they must design a bumper to attach to the cart. This also aligns with NGSS Standard MS-PS2-1.
The crash cushions or bumpers can be built out of an assortment of basic arts and craft supplies. Construction paper, paper cups, cotton balls, dice, are good materials.
The experiment investigates concepts in force and motion, including Newton’s Third Law and impulse. In the design process of the cushions or bumpers, students have opportunities to test and iterate on their designs to find better solutions based on the evidence collected (data and observations). The lab asks students to conclude why certain designs were better than others based on evidence and scientific reasoning (ideas, principles, and theories in force, motion, and other concepts).
Materials
-PocketLab Voyager
-PocketLab HotRod or other dynamics cart
-Cardboard box
-Ramp
-Misc. materials for crash cushion design: dice, construction paper, scissors, masking tape, staples
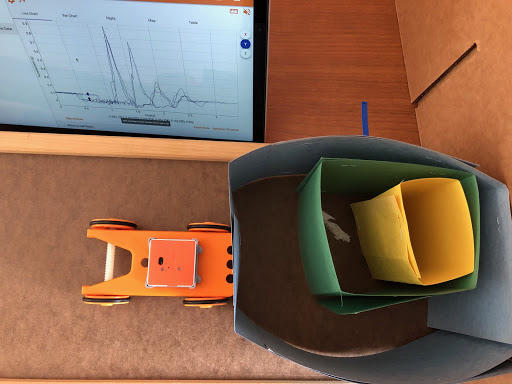
Materials Setup
Using the set up from the image generally gives the best results. Make sure the students know which axis and in which direction the impact acceleration will be measured. Check out example data, images, and videos below for more help.
Lesson Links
Crash Cushion Investigation 1 (Construction Paper Only)
Crash Cushion Investigation 2 (Construction Paper Cushion Design, Misc. Material Cushion Design, Materials Cost Extension)
Crash Cushion Investigation 3 (Using Dice for Crash Cushion Design)
Crash Cushion Design at the Society of Women Engineers at Santa Clara University
Scientific Principles
Essentially, crash cushions that deform and compress at impact will more gradually slow the car down. The cushions should increase the total time of the collision itself. This will reduce the magnitude of the force experienced by the car as the collision isn’t as quick or sudden. If you want to take the scientific reasoning even further, students can investigate why this is by looking at impulse.
Impulse is the change in momentum of an object. Whether the car is crashing into a wall or a crash cushion, the change in momentum of the car should be the same. If the experiment is properly controlled, the car will crash with the same momentum (mass times velocity) and then, after the crash, come to a stop (zero momentum). Therefore, if the cart is crashing directly into the wall or into any of the crash cushions, the impulse (change in momentum) for every crash will always be the same.
Equation for impulse: J=F· ∆t where J=impulse F=force ∆t=change in time
An effective crash cushion will increase the time of the collision (∆t) which will reduce the force (F) of the collision. This is because when looking at the equation for impulse, F and ∆t are inversely proportional. You can also observe this in the data. With an effective crash cushion, the impact “spikes” measured in the acceleration graph are wider along the time axis (x-axis) with a smaller magnitude along the acceleration axis (y-axis).
Example Data:
Control Crash Data
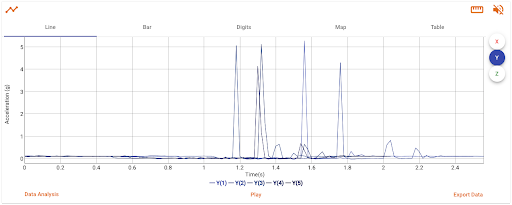
Data from 5 trials with the car crashing into a cardboard wall. Notice the time of the impact “spikes” are quick and sudden. The impact acceleration is high.
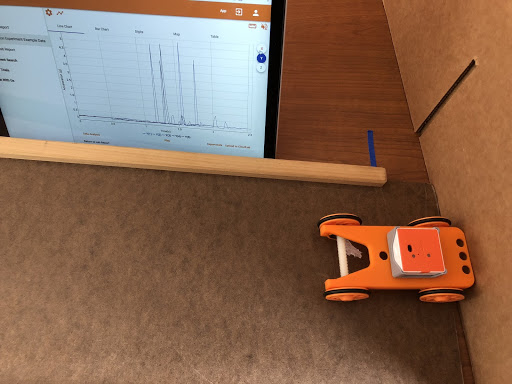
Data for Triangle Crash Cushion Design
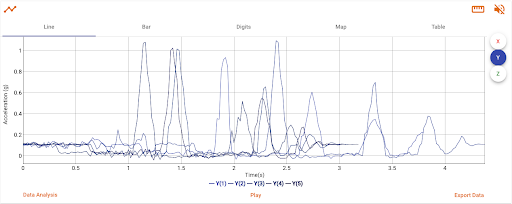
Data from 5 trials with the design pictured. Notice the time of the impact “spikes” have increased. The impact acceleration has reduced.

Nesting Rectangle Crash Cushion Design
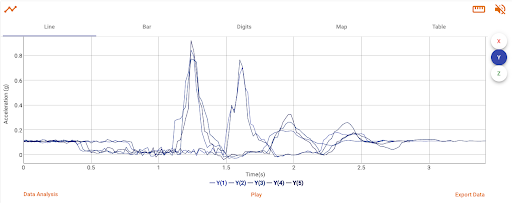
Data from 5 trials with the design pictured. Notice the time of the impact "spikes" have increased again. The impact acceleration has reduced even more.
Extensions
Real-world engineers must often balance the performance of a design with how practical it is to implement. There are multiple extensions to this experiment to model this challenge. One extension is to give each crash cushion supply a material cost and have students engineer a design that must meet a specific budget along with a performance metric. Another extension is to design a cushion that will meet a performance metric even after the cushion has been damaged from previous crashes. In the real-world, crash cushions can be difficult to replace after a crash. A second car may crash into the already damaged crash cushion before it is replaced, making a crash cushion that continues to be effective after damage more helpful.
NGSS Alignment
Performance Expectation: MS-PS2-1
Apply Newton’s Third Law to design a solution to a problem involving the motion of two colliding objects. (Clarification Statement: Examples of practical problems could include the impacts of collisions between two cars, between a car and stationary objects and between a meteor and a space vehicle) (Assessment Boundary: Assessment is limited to vertical or horizontal interactions in one dimension).
The three pillars of the above performance expectation are:
Science and Engineering Practices: Constructing explanations and designing solutions.
Disciplinary Core Ideas: PS2.A: Forces and Motion (Newton’s Third Law)
Crosscutting Concepts: Systems and System Models


