Introduction
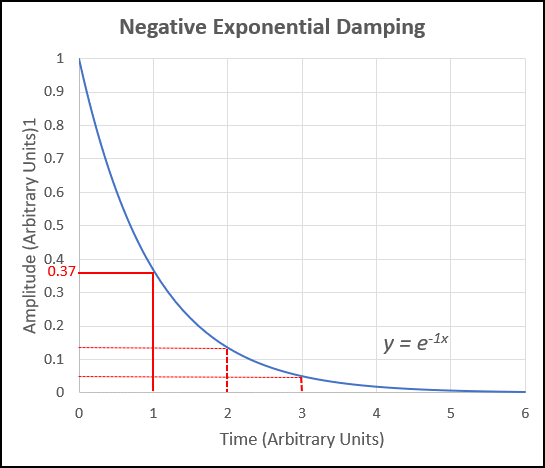
Damping causes oscillatory systems to dissipate energy to their surroundings. Frictional losses are quite common in mechanical systems and result in damped simple harmonic motion. For example, when a child stops pumping a swing, the amplitude of the oscillations gradually decay toward zero. The same thing happens to a mass that hangs from an oscillating spring. It is quite common for the amplitude of such oscillations to exhibit a behavior that is negative exponential over time, as shown in Figure 1. The graph indicates that if we take the amplitude at time t=0 to be 1, then the amplitude at time t=1 is 1/e (0.37) of its value at time t=0. In other words, the amplitude decrease by 37% of its current value every 1 unit of time. For example, at time t=2, the amplitude would be 0.37 x 0.37 = 0.137 arbitrary units. At time t=3, the amplitude would be 0.137 x 0.37 = 0.05 arbitrary units. The time interval τ during which the amplitude drops to 1/e of its initial value is known as mean lifetime of the oscillation.
Our Exponential Damping Experiment
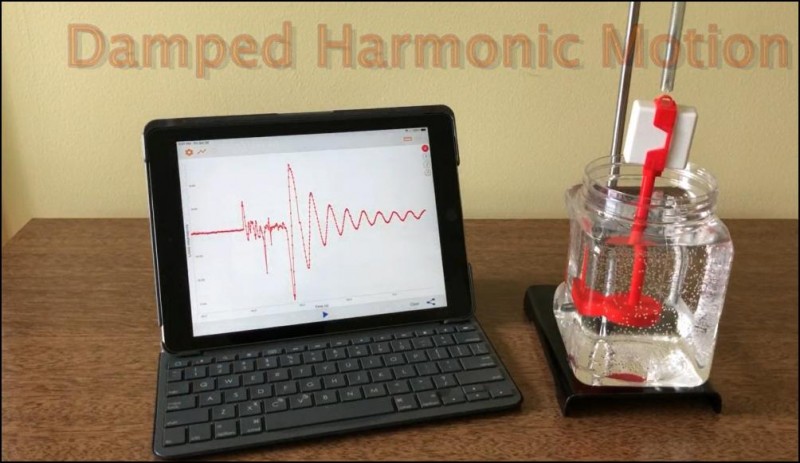
Because damped simple harmonic motion is so common, many experiments can be designed to study it. In this experiment we will make use of PocketLab Voyager's accelerometer to investigate how acceleration dampens over time. Figure 2 shows the experiment setup. A 5 N/m spring is suspended from a ring stand. The spring can be purchased here. A 3D printed holder for Voyager and damper are suspended from the spring. The damper is inserted into a container of liquid. The author used water for one run of the experiment and canola oil for a second run, allowing for the study of two different mean lifetimes for damped simple harmonic motion. The damper is pulled down and then released, allowing up-and-down motion of Voyager. Voyager's accelerometer data is captured by the PocketLab app, as shown on the iPad screen.

The 3D printer STL files accompany this lesson. Figure 3 shows the two parts - the PocketLab holder and the damper. The damper (right) screws into the nut that is built into the PocketLab holder (left). Note that it is important to print the holder at 100% infill so that it will sink better in the liquid into which it immersed.

Performing the Experiment
Probably the best way to learn how to perform the experiment is to observe the short video below. PocketLab has been oriented in its holder so that the positive x direction is down, and x-acceleration is of interest. The data rate in the PocketLab app is set to 50 points/sec and recording is turned on. PocketLab and the damper are pressed down and released. After the amplitude has reduced close to zero, recording is stopped and the graph is repositioned on the screen. The amplitude appears to show exponential damping, but can then be downloaded for verification and further spreadsheet analysis.
Damped Simple Harmonic Motion Analysis
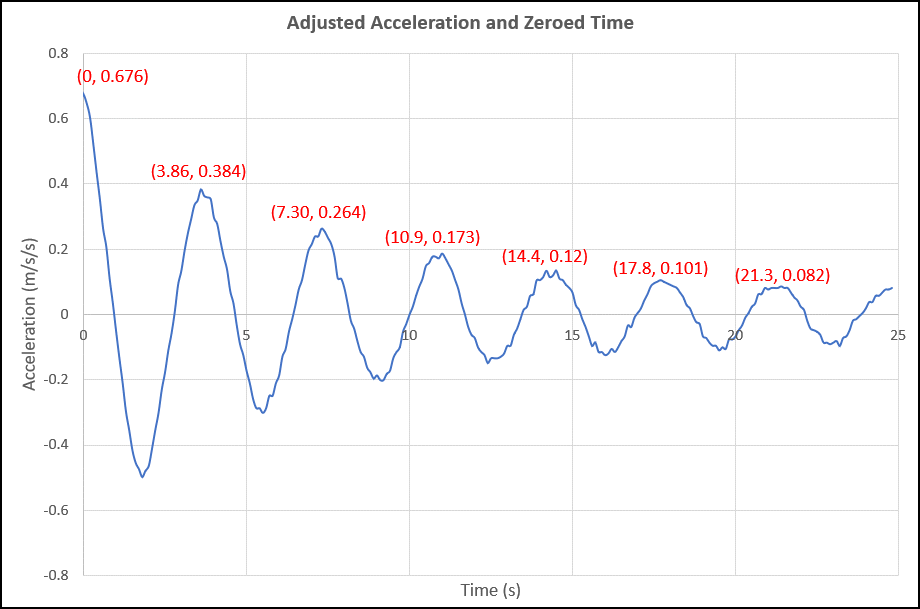
Figure 4 contains an Excel graph of x-acceleration data from the PocketLab app after it has been adjusted so that (1) the acceleration is zero when the damper is at rest, and (2) the zero of time is taken when the amplitude is at its first relative maximum. In order to determine if the damping is negative exponential, we need to determine the (time, acceleration) coordinates for each relative maximum in the graph. These coordinates are shown in red in the graph of Figure 4.
Finally, we make an Excel graph of damped harmonic motion for the relative maxima, as shown in Figure 5. The trend line feature of Excel is used, and exponential is selected. The fit appears good and has an R-squared value of 0.97. The graph provides solid evidence that the acceleration experiences negative exponential damping as the PocketLab HotRod bounces magnetically. It is a good idea to have the class suggest what non-conservative forces are responsible for this damping. Which of these forces are likely the biggest contributors to the damping?
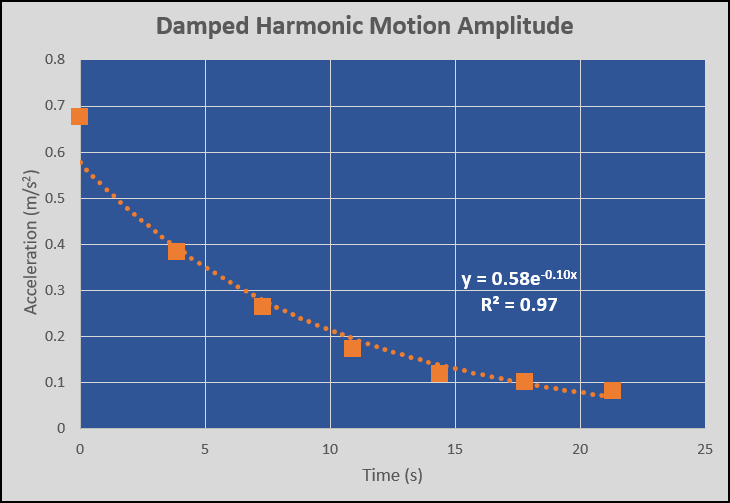
In general, y = Ao exp(-Ct), where Ao is the initial amplitude. In the graph of Figure 5, Ao = 0.58 and C = 0.10. Have your students prove that the mean lifetime τ = 1/C. (Hint: take the natural log of both sides of the equation y = Ao exp(-Ct). In the graph of Figure 5, the mean lifetime is τ = 1/C = 1/0.10 = 10 seconds. The amplitude drops by 1/e of its current value every 10 seconds.
Additional Investigation on Damped Simple Harmonic Motion
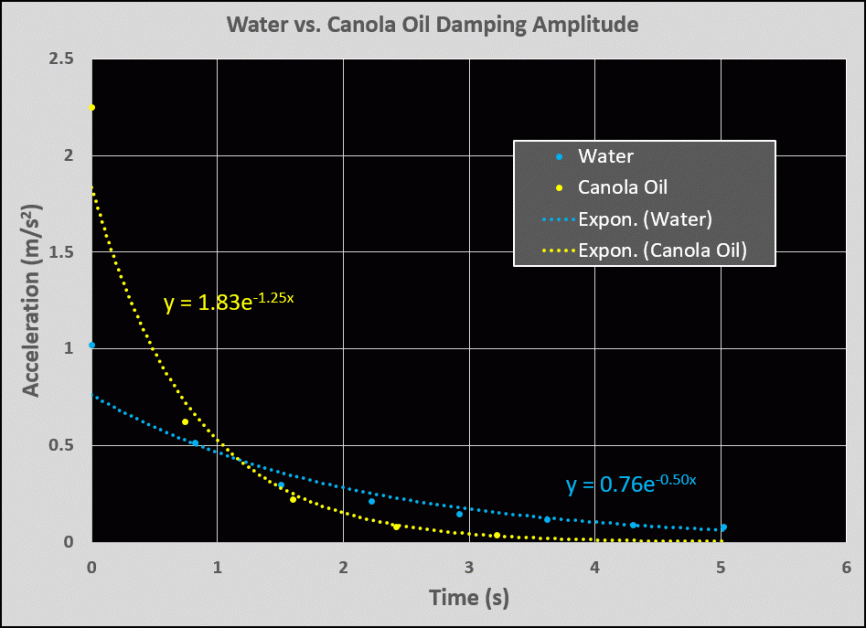
It is instructive for students to compare damped simple harmonic motion with two fluids, say water and canola oil. Figure 6 shows the setup for these two fluids used by the author of this lesson.

Figure 6 contains a graph comparing damping with water versus damping with canola oil from PocketLab data obtained by the author. The large dots are data from PocketLab, while the dotted lines are exponential fits to the data. Here, the students can compare the mean lifetime for water versus oil.
Another Lesson on Damped Motion
If you want to look at another approach to damped motion, check out this lesson:
The Negative Exponential Nature of Damping
This lesson looks at damping of a PocketLab HotRod as it bounces back-and-forth on an incline.